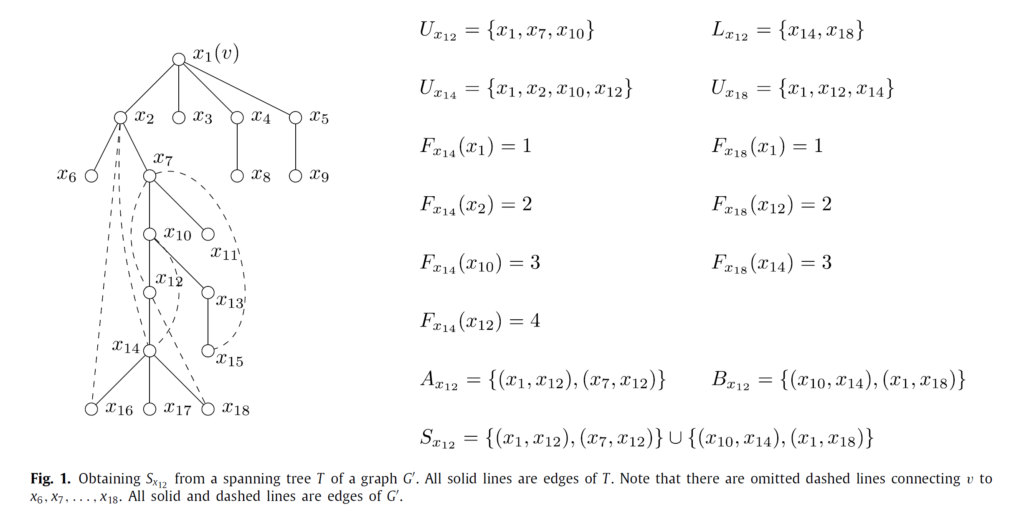In the Minimum Spanning Tree Cycle Intersection (MSTCI) problem, the objective is to find a spanning tree with minimum tree intersection number among all possible spanning trees. Dubinsky et al. (2021) proposed the MSTCI problem recently and showed that a star spanning tree, which is a spanning tree with one vertex connecting to all other vertices, has the minimum tree intersection number in complete graphs. Dubinsky et al. proposed that, if a graph admits a star spanning tree, then the star spanning tree has the minimum tree intersection number.
According to the paper published by Prof. Kun-Mao Chao and Min-Jen Chen in June 2022, it not only confirms this conjecture, but also expands its possibilities: “Not only the complete graph, but whenever a graph has a star spanning tree, it has the minimum tree intersection number.” In other words, given a graph G and T be a spanning tree of G. Every edge e in G − T induces a cycle in T ∪ {e}, which is called cycle-edges, while the cycle induced by a cycle-edge is called a tree-cycle. The intersection of two tree-cycles is the set of all edges in common. If the intersection of two different tree-cycles is non-empty, it is considered as one intersection, and the number of tree intersections of the spanning tree T is the number of intersections of all its tree-cycles. MSTCI problem is aim to find a spanning tree with minimum tree intersection number among all possible spanning trees. Dubinsky et al. proposed a conjecture which states that if a graph has a star spanning tree, then this spanning tree has the minimum number of tree intersections. In the paper, Prof. Chao and Chen prove this conjecture and explore the possibility of its extension.
In this paper, S_{x_*} is the core part of the construction approach (see the attached figure). The loop edges in a single S_{x_*} have cycle intersections with each other, and the intersection of any two S_{x_i} and S_{x_j} is less than 1, which ensures that the intersection of tree-cycles computed in a single S_{x_*} will not be computed repeatedly. By summing the pairwise intersections within S_{x_*}, it can be proved that the total number of intersections of any tree-cycle (minus the inter-branch loop edge) has a lower bound, and it is not lower than the total number of cycle intersections of any star spanning tree. As a result, Prof. Chao and Chen confirmed the conjecture proposed by Dubinsky et al. that if a graph has a star spanning tree, i.e., a spanning tree in which one point is adjacent to all other points, then this star spanning tree has the minimum number of tree intersections.
研究主題:最小生成樹環交集假設證明
撰寫:學生王馨
在最小生成樹環交集 (Minimum Spanning Tree Cycle Intersection,簡寫為MSTCI) 的問題中,目標是在所有可能的生成樹中找到具有最小樹交集數 (tree intersection number) 的生成樹。Dubinsky等人 (2021) 最近提出了MSTCI問題,並表明星形生成樹 (star spanning tree),即其中一點和其他所有點都相鄰的生成樹,在完全圖 (complete graph) 中會具有最小的樹交集數。Dubinsky等人提出假設,若一圖 (graph) 為星形生成樹,則此生成樹將具有最小樹交集數。
根據趙教授與陳泯臻同學於2022年6月發表的論文,其不僅證實了此猜想成立,更擴展了其可能性:「不只是完全圖,只要一圖裡有星形生成樹,它就有最小的樹交集數。」換句話說,給定一圖G 和其一生成樹T,每條在G − T 的邊 (e) 會在T ∪ {e} 中產生一個環,將這些邊稱作環邊,而該環則稱作樹環。兩個樹環的交集為其所有共有的邊形成的集合,若兩相異樹環的交集是非空的,則將其視為一次交集,而生成樹T 的樹交集數為其所有樹環的交集次數。最小生成樹環交集問題旨在找出圖的所有生成樹中樹交集數最小的生成樹。Dubinsky 等人提出一猜想,此猜想敘述為若一圖有一星形生成樹,則此星形生成樹有最小的樹交集數。在論文中,趙教授與陳同學證明此猜想,並探討其延伸的可能性。
在該論文中,S_{x_*}為建構方式的核心部分 (可參考附圖),單一S_{x_*}內的迴圈邊彼此皆有樹環交集 (cycle intersection),而任兩個S_{x_i}和S_{x_j}的交集個數小於1,可保證在單一S_{x_*}內計算的樹環交集不會被重複計算。如此就可藉由S_{x_*}內部的成對交集n總和,證明任何生成樹 (扣掉內部分支之迴圈邊) 的樹環交集總數都有一個下限,而其不會低於任何星形生成樹的樹環交集總數。由此,趙教授與陳同學證實Dubinsky等人所提出的猜想,若一圖有一星形生成樹,即其中一點和其他所有點都相鄰的生成樹,則此星形生成樹有最小的樹交集數。